Module Top-100-Liked

11.盛最多水的容器

438.找到字符串中所有字母异位词 ✅

3.无重复字符的最长子串 ✅

283.移动零 ✅

15.三数之和 ✅

34.在排序数组中查找元素的第一个和最后一个位置 ✅

153.寻找旋转排序数组中的最小值 ✅

287.寻找重复数 ✅

74.搜索二维矩阵 ✅

33.搜索旋转排序数组 ✅

35.搜索插入位置 ✅

39.组合总和

22.括号生成 ✅

17.电话号码的字母组合 ✅

51.N皇后 ✅

131.分割回文串 ✅

46.全排列 ✅

78.子集 ✅

79.单词搜索 ✅

70.爬楼梯 ✅

322.零钱兑换 ✅

198.打家劫舍 ✅

300.最长递增子序列 ✅

5.最长回文子串 ✅

152.乘积最大子数组 ✅

53.最大子数组和 ✅

64.最小路径和 ✅

416.分割等和子集 ✅

279.完全平方数 ✅

49.字母异位词分组 ✅

128.最长连续序列 ✅

1.两数之和 ✅

前缀积 + 后缀积

739.每日温度【单调栈】

本质上是在一个数组当中不断寻找右边第一个比当前数大的。通过维持一个从栈底到栈顶单调递减的栈，栈里放着所有没找到右边第一个比自己大的元素的元素。不断查看当前数和单调栈的栈顶元素，如果当前数大于栈顶元素，那么栈顶元素就是找到了右边第一个比自己大的元素，于是结算。

394.字符串解码【栈】

表达式有层次关系的字符串要想办法用“栈”。这题涉及数字和字母，所以用双栈，同时看到「[」保存状态、重置状态，看到「]」恢复状态、处理。（本质：状态机思维，碰到一类字符先累加状态。）

84.柱状图中最大的矩形【单调栈】

假设当前枚举到的柱子高度是构成矩形的高度。我们需要尽可能大的扩展宽度。因此我们不断往左和右扩展矩形，碰到大于等于当前枚举到的柱子高度，我们继续扩展，否则停止扩展。

但是我们发现扩展的过程其实就是在左右两侧寻找比第一根当前柱子矮的柱子。因此我们想到使用单调栈来处理这个问题。

155.最小栈【单调栈】

用两个栈，一个栈用来放数字，一个单调栈用来放当前的最小值。

42.接雨水【单调栈】

单调栈的做法可以想象成在填水泥。维护一个从栈底到栈顶递减的单调栈。当发现当前入栈柱子高度比栈顶柱子高度大时，说明找到了右边界。于是我们尝试找左边第一个比栈顶柱子高度大的柱子，这个柱子就是左边界。怎么找呢？其实只需要看栈是否出栈后还有元素没，有的话栈顶就是左边界。这样一来只需要比较左右边界的最小值，然后减去当前柱子高度，要填的水泥高度。

20.有效的括号【栈】

利用栈的先进后出特性，维护一个栈，遇到左括号就入栈，遇到右括号就出栈，然后判断出栈的左括号是否和右括号匹配。为了做到匹配这件事，我们还需要一个map记录右括号到左括号的映射关系。

2.两数相加【遍历链表】

按照加法运算的规则，从低位开始相加，如果相加结果大于10，则进位。

138.随机链表的复制【特殊结构】

深拷贝随机链表，使用双Map + 两次链表遍历。一个oldToNew记录旧节点与新节点的映射，一个newToOld记录新节点与旧节点的映射。其中：

• newToOld用来从新节点找到旧节点。
• oldToNew用来从旧random节点找到新random节点。

160.相交链表【遍历链表】

双指针解法，本质是构造两条等长链表。假设a长度为lenA，b长度为lenB，共同长度为lenC，补齐各自缺少对方的节点，构造出两条同样长的新链表。 则lenA + lenC + lenB = lenB + lenC + lenA。 由于a和b两个走的路程是一样长的，把相交节点叫NodeC，则a，b两者走到的终点就是NodeC。其中NodeC可以是一个节点或者null空节点。

// A: 1 -> 2 -> 3 
//               -> C -> 4 -> 5 -> null
// B: 6 -> 7 
// A + B: 1 -> 2 -> 3 -> C(相交点) -> 4 -> 5 -> null -> 6 -> 7 -> C(相交点) -> 4 -> 5 -> null
// B + A: 6 -> 7 -> C(相交点) -> 4 -> 5 -> null -> 1 -> 2 -> 3 -> C(相交点) -> 4 -> 5 -> null
Copy

141.环形链表【快慢指针】

龟兔赛跑，乌龟一次走1步，兔子一次走2步。如果链表有环，那么兔子一定会追上乌龟。因为乌龟相对于兔子来说是静止的，兔子对乌龟来说每次都在前进一步。有环的话，兔子会比乌龟先进环，等到乌龟进环的时候，假如两者相差距离为n，那么兔子在环里走n步就能追上乌龟。因为我们说了，兔子相对于乌龟来说每次都在前进一步，所以n步就能追上乌龟。

142.环形链表II【快慢指针】

146.LRU缓存【特殊结构】

哈希表+循环双链表

• 空链表时：dummy ⇄ dummy

• 插入节点A后：dummy ⇄ A ⇄ dummy

• 插入节点B后：dummy ⇄ B ⇄ A ⇄ dummy

• 删除节点A后：dummy ⇄ B ⇄ dummy

• 删除节点B后：dummy ⇄ dummy

23.合并K个升序链表【分治思想】

21.合并两个有序链表【合并链表】

尾插法，两个链表谁小谁就插到新链表的后面，直到两个链表合并完成。

234.回文链表【反转链表】

寻找链表的中间节点【快慢指针】 + 反转链表【头插法】 + 对比反转部分和原链表剩余部分。

19.删除链表的倒数第N个结点【删除链表】

• 假设一把尺子，l代表尺子的左边，r代表尺子的右边。那么假如从l到r有m个节点，我们把这把尺子的右边对齐整条链表的右边。那么从左往右数是1到m个节点，则从右往左数肯定也是1到m个节点。因此，如果你要删除倒数第m个节点的话，那么l就是倒数第m个节点。

• 为了删除掉节点B，我们需要找到B之前的节点A，通过A.next = A.next.next来删除B节点。

• 为了解决链表长度为1的情况，我们还需要使用一个虚拟头节点来解决这个问题。

206.反转链表【链表反转】

设计三个指针pre、cur、nxt。其中pre指向当前节点的前一个节点，cur指向当前节点，nxt指向当前节点的下一个节点。利用头插法完成反转。这样一想，我们就能够知道pre、cur、nxt的另一层意思：

• pre代表新链表的头节点
• cur代表准备插入到新链表的节点
• nxt代表下一个准备插入到新链表的节点。

25.K个一组翻转链表【反转链表】

“反转链表的一部分”跟“反转整条链表”不少操作是类似的。反转同样需要运用到三个指针pre、cur、nxt。其中pre指向当前节点的前一个节点，cur指向当前节点，nxt指向当前节点的下一个节点。利用头插法完成反转。

相对于“反转整条链表”，“反转链表的一部分”需要应用到一些性质：

• 反转链表部分结束之后，pre就是反转部分链表的头部。而cur在pre后边，它代表着反转部分的右边头部。
• 我们把反转部分链表的尾部的前一个节点叫做p0，p0的next指向反转好的链表的尾部。 因此，反转完链表的部分后，我们还需要把p0的next节点的next指向cur，然后让p0的next指向pre，这样子才算完成了链表部分反转。

特殊情况，当left为1的时候，反转部分的前一个节点是无法找到p0的，为了统一逻辑，我们引入一个虚拟头节点dummy，让dummy的next指向head。这样子我们就可以认为当left为1的时候，p0就是dummy。

148.排序链表【分治思想】

寻找链表的中间节点【快慢指针】的同时将链表分成两部分 + 归并排序【合并两个有序链表】。

24.两两交换链表中的节点【反转链表】

K个一组反转链表k=2的特殊情况，。

94.二叉树的中序遍历【DFS】

二叉树的中序遍历顺序是：左根右

102.二叉树的层序遍历【DFS】

层序遍历就是按照层级从上到下，从左到右遍历二叉树。它还有个名字叫广度优先搜索（BFS）。

124.二叉树中的最大路径和【DFS】

对于当前节点node，该节点的处的max值可能： 1、当前节点和两侧节点都要 2、当前节点和左右当中一侧的节点 3. 如果两侧贡献值都是负数，越加越小，那么直接不要两侧，也就是取0

199.二叉树的右视图【BFS】

BFS 层序遍历，每一层收集最右边的节点。

105.从前序与中序遍历序列构造二叉树【DFS】

• 利用前序遍历确定根节点，利用中序遍历确定左右子树的范围，通过递归构建二叉树。
• 为了方便查找中序遍历的根节点，使用哈希表存储中序遍历的值和索引，建立值到索引的映射。

108.将有序数组转换为二叉搜索树【DFS】

二叉搜索树的中序遍历的结果就是一个升序的数组。通过二分查找，每次都找到数组的中间节点作为根节点，然后递归处理左右子树。

543.二叉树的直径【DFS】

从子树中的叶子节点到当前节点的路径叫做“链”。遍历每一个节点，然后在每一层计算当前子树的最大链长，然后加上1，形成当前子树的左侧链长和右侧链长，然后更新最大值。

                 1
   dfs(l)+1     / \    dfs(r)+1
               2   3
              / \   \
             4   5   6
Copy

114.二叉树展开为链表【DFS】

核心思路：利用前序遍历将二叉树展开为链表，使用全局指针 cur 追踪链表末尾，按前序遍历顺序连接所有节点。

关键点：

• 使用虚拟节点作为链表起始点
• 前序遍历确保节点按正确顺序连接
• 将每个节点的 left 设为 null，right 连接下一个节点

226.翻转二叉树【DFS】

翻转二叉树，就是将二叉树的左右子树交换。

230.二叉搜索树中第K小的元素【DFS】

利用二叉搜索树的中序遍历结果是升序的特性，则第K小的元素就是中序遍历的第K个元素。

236.二叉树的最近公共祖先【DFS】

利用递归遍历二叉树，如果当前节点是p或q之一，或者p、q分别在左右子树中，则当前节点就是最近公共祖先。否则继续在包含p、q的子树中递归查找。

104.二叉树的最大深度【DFS】

二叉树的深度就是所有的根节点到叶子节点的节点数的最大值。

437.路径总和III【DFS】

• 与“和为K的连续子数组”解法一致。将每个遍历到的node作为终点，统计有多少个起点到终点node的路径总和恰好等于targetSum。再转化成前缀和问题。
• 给了“路径”限制：从上到下，也就是父到子的方向。
• DFS 遍历这棵树，遍历到节点 node 时，假设 node 是路径的终点，那么有多少个起点，满足起点到终点node的路径总和恰好等于targetSum

101.对称二叉树【DFS】

如果一颗二叉树的所有子树的左右子树都轴对称，那么这棵二叉树就轴对称。

98.验证二叉搜索树【DFS】

利用二叉搜索树的中序遍历结果是升序的特性，来判断是否是二叉搜索树。

三色标记法 + dfs

Trie树

四个方向dfs插旗

48.旋转图像【matrix】

观察交换规律，看成上下左右，每个方向控制几个数。比如3*3的矩阵，上下左右分别控制2个数。t, b, l, r 指针围成一个圈，t控制上，b控制下，l控制左，r控制右。比如：

。

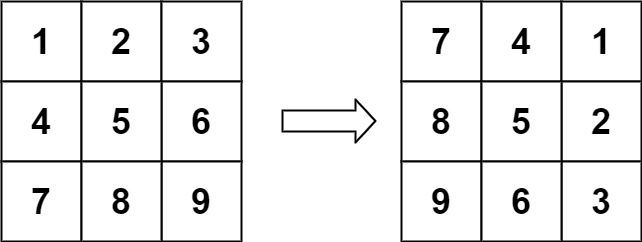可以看成是t控制了第一排前两个数(1, 2)，r控制了最后一列的前两个数(3, 6)。b控制了最后一排从右数的两个数(9, 8)，l控制第一列的从下数的前两个数(7, 4)。错开来看，规律就出来了：

• 第1轮-第1次

  • 坐标在 (b + 0, l) 的元素来到坐标在 (t, l + 0) 的元素位置，
  • 坐标在 (t, l) 的元素来到坐标在 (t, r) 的元素位置，
  • 坐标在 (t + 0, r) 的元素来到坐标在 (b, r) 的元素位置。

• 第1轮-第2次

  • 坐标在 (b + 1, l) 的元素来到坐标在 (t, l + 1) 的元素位置
  • 坐标在 (t, l + 1) 的元素来到坐标在 (t + 1, r) 的位置
  • 坐标在 (t + 1, r) 的元素来到坐标在 (b, r - 1) 的位置

次数的确定由 r - l 决定，或者 b - t 决定。而具体进行多少轮？只要 b > t && l < r 就继续，否则停止。

240.搜索二维矩阵II【matrix】

从右上角开始找，这样子判断一个数要么比target大，要么比target小，要么就是target。

• 比target大，说明当前数所在列一定不可能了，因为这列最小的数都比target要大了，把这列消除掉
• 比target小，说明当前数所在行一定不可能了，因为这行最大的数都比target要小了，把这行消除掉

重复上述过程，消除行、消除列。直到找到为止或者越界为止。

73.矩阵置零【matrix】

• 原地解法：利用矩阵本身作为辅助空间，将需要置零的行和列标记为 Infinity，最后再遍历矩阵将 Infinity 置零。
• 辅助空间解法：利用辅助空间记录需要置零的行和列，最后再遍历矩阵将需要置零的行和列置零。

54.螺旋矩阵【matrix】

• 设定t,b,l,r四个边界分别代表上、下、左、右，同时也代表一个圈，每次将整个圈遍历完，然后更新边界，缩小这个圈。
• 接下来根据不同解法，有不同的实现方式：
  • 标记解法：将已经访问过的元素标记为 Infinity，不需要判断越界的情况。
  • 不标记解法：在遍历的过程当中还要判断越界的情况，比如只有一行，或者一列，t更新后，t>b，或者l更新后，l>r，那么就说明没有下一圈了，直接退出。不然会导致重复遍历。