如果你刚开始刷题,还不熟悉基本编程语法和常用库函数,推荐先刷力扣官方的入门题单:
有了一些简单题的积累,就可以开始刷我的题单啦~
下面的题目已按照难度分排序,右侧数字为难度分。
在刷题的过程中,如果遇到难度很大,题解都看不懂的题目,建议直接收藏,过段时间再来做。
一、定长滑动窗口
§1.1 基础
- 1456. 定长子串中元音的最大数目 1263
- 643. 子数组最大平均数 I
- 1343. 大小为 K 且平均值大于等于阈值的子数组数目 1317
- 2090. 半径为 k 的子数组平均值 1358
- 2379. 得到 K 个黑块的最少涂色次数 1360
- 2841. 几乎唯一子数组的最大和 1546
- 2461. 长度为 K 子数组中的最大和 1553
- 1423. 可获得的最大点数 1574
- 1052. 爱生气的书店老板
- 1652. 拆炸弹 做到 O(n)
- 1176. 健身计划评估(会员题)
- 1100. 长度为 K 的无重复字符子串(会员题)
- 1852. 每个子数组的数字种类数(会员题)
- 1151. 最少交换次数来组合所有的 1(会员题)
- 2107. 分享 K 个糖果后独特口味的数量(会员题)
§1.2 进阶(选做)
- 3439. 重新安排会议得到最多空余时间 I 1729
- 2134. 最少交换次数来组合所有的 1 II 1748
- 1297. 子串的最大出现次数 1748
- 2653. 滑动子数组的美丽值 1786
- 1888. 使二进制字符串字符交替的最少反转次数 2006
- 567. 字符串的排列
- 438. 找到字符串中所有字母异位词
- 30. 串联所有单词的子串
- 2156. 查找给定哈希值的子串 2063
- 2953. 统计完全子字符串 2449
- 1016. 子串能表示从 1 到 N 数字的二进制串 做到 O(∣s∣)
- 683. K 个关闭的灯泡(会员题)做到 O(n)
- 2067. 等计数子串的数量(会员题)
- 2524. 子数组的最大频率分数(会员题)
§1.3 其他(选做)
二、不定长滑动窗口
不定长滑动窗口主要分为三类:求最长子数组,求最短子数组,以及求子数组个数。
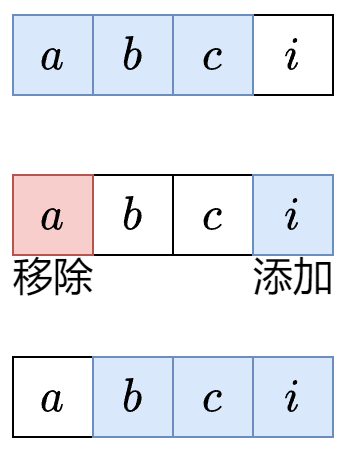
注:滑动窗口相当于在维护一个队列。右指针的移动可以视作入队,左指针的移动可以视作出队。
§2.1 求最长/最大
§2.1.1 基础
- 3. 无重复字符的最长子串
- 3090. 每个字符最多出现两次的最长子字符串 1329
- 1493. 删掉一个元素以后全为 1 的最长子数组 1423
- 1208. 尽可能使字符串相等 1497
- 904. 水果成篮 1516
- 1695. 删除子数组的最大得分 1529
- 2958. 最多 K 个重复元素的最长子数组 1535
- 2024. 考试的最大困扰度 1643
- 1004. 最大连续 1 的个数 III 1656
- 1658. 将 x 减到 0 的最小操作数 1817
§2.1.2 进阶(选做)
- 2730. 找到最长的半重复子字符串 非暴力做法
- 2779. 数组的最大美丽值 1638
- 1838. 最高频元素的频数 1876
- 2516. 每种字符至少取 K 个 1948
- 2831. 找出最长等值子数组 1976
- 2271. 毯子覆盖的最多白色砖块数 2022
- 2106. 摘水果 2062
- 2555. 两个线段获得的最多奖品 2081
- 2009. 使数组连续的最少操作数 2084
- 1610. 可见点的最大数目 2147
- 2781. 最长合法子字符串的长度 2204
- 3411. 最长乘积等价子数组 非暴力做法约 2300
- 3413. 收集连续 K 个袋子可以获得的最多硬币数量 2374
- 2968. 执行操作使频率分数最大 2444
- 1040. 移动石子直到连续 II 2456
- 395. 至少有 K 个重复字符的最长子串
- 1763. 最长的美好子字符串 非暴力做法
- 487. 最大连续 1 的个数 II(会员题)
- 159. 至多包含两个不同字符的最长子串(会员题)
- 340. 至多包含 K 个不同字符的最长子串(会员题)
§2.2 求最短/最小
- 209. 长度最小的子数组
- 2904. 最短且字典序最小的美丽子字符串 做到 O(n2)
- 1234. 替换子串得到平衡字符串 1878
- 2875. 无限数组的最短子数组 1914
- 76. 最小覆盖子串
- 632. 最小区间 做法不止一种
§2.3 求子数组个数
§2.3.1 越长越合法
一般要写 ans += left。
内层循环结束后,[left,right] 这个子数组是不满足题目要求的,但在退出循环之前的最后一轮循环,[left−1,right] 是满足题目要求的。由于子数组越长,越能满足题目要求,所以除了 [left−1,right],还有 [left−2,right],[left−3,right],…,[0,right] 都是满足要求的。也就是说,当右端点固定在 right 时,左端点在 0,1,2,…,left−1 的所有子数组都是满足要求的,这一共有 left 个。
- 1358. 包含所有三种字符的子字符串数目 1646
- 2962. 统计最大元素出现至少 K 次的子数组 1701
- 3325. 字符至少出现 K 次的子字符串 I 做到 O(n)
- 2799. 统计完全子数组的数目 做到 O(n)
- 2537. 统计好子数组的数目 1892
- 3298. 统计重新排列后包含另一个字符串的子字符串数目 II 1909 同 76 题
- 2495. 乘积为偶数的子数组数(会员题)
§2.3.2 越短越合法
一般要写 ans += right - left + 1。
内层循环结束后,[left,right] 这个子数组是满足题目要求的。由于子数组越短,越能满足题目要求,所以除了 [left,right],还有 [left+1,right],[left+2,right],…,[right,right] 都是满足要求的。也就是说,当右端点固定在 right 时,左端点在 left,left+1,left+2,…,right 的所有子数组都是满足要求的,这一共有 right−left+1 个。
- 713. 乘积小于 K 的子数组
- 3258. 统计满足 K 约束的子字符串数量 I 做到 O(n)
- 2302. 统计得分小于 K 的子数组数目 1808
- 2762. 不间断子数组 1940
- LCP 68. 美观的花束
- 2743. 计算没有重复字符的子字符串数量(会员题)
思维扩展(选做)
- 3134. 找出唯一性数组的中位数 2451
- 3261. 统计满足 K 约束的子字符串数量 II 2659 子串的子串
§2.3.3 恰好型滑动窗口
例如,要计算有多少个元素和恰好等于 k 的子数组,可以把问题变成:
- 计算有多少个元素和 ≥k 的子数组。
- 计算有多少个元素和 >k,也就是 ≥k+1 的子数组。
答案就是元素和 ≥k 的子数组个数,减去元素和 ≥k+1 的子数组个数。这里把 > 转换成 ≥,从而可以把滑窗逻辑封装成一个函数 f,然后用 f(k) - f(k + 1) 计算,无需编写两份滑窗代码。
总结:「恰好」可以拆分成两个「至少」,也就是两个「越长越合法」的滑窗问题。
注:也可以把问题变成 ≤k 减去 ≤k−1(两个至多)。可根据题目选择合适的变形方式。
注:也可以把两个滑动窗口合并起来,维护同一个右端点 right 和两个左端点 left1 和 left2,我把这种写法叫做三指针滑动窗口。
- 930. 和相同的二元子数组 1592
- 1248. 统计「优美子数组」 1624
- 3306. 元音辅音字符串计数 II 2200
- 992. K 个不同整数的子数组 2210
§2.4 其他(选做)
- 1438. 绝对差不超过限制的最长连续子数组 1672
- 825. 适龄的朋友 1697
- 2401. 最长优雅子数组 1750
- 1156. 单字符重复子串的最大长度 1787 有简单做法
- 424. 替换后的最长重复字符
- 438. 找到字符串中所有字母异位词 有定长滑窗/不定长滑窗两种写法
- 1712. 将数组分成三个子数组的方案数 2079
- 1918. 第 K 小的子数组和(会员题)
⚠ 滑窗的内容到这里就结束了,可以去刷下一个题单。
刷题路线请看 如何科学刷题。
三、单序列双指针
§3.1 相向双指针
两个指针 left=0, right=n−1,从数组的两端开始,向中间移动,这叫相向双指针。上面的滑动窗口相当于同向双指针。
- 344. 反转字符串
- 125. 验证回文串
- 1750. 删除字符串两端相同字符后的最短长度 1502
- 2105. 给植物浇水 II 1507
- 977. 有序数组的平方 做到 O(n)
- 658. 找到 K 个最接近的元素
- 1471. 数组中的 K 个最强值 用双指针解决
- 167. 两数之和 II - 输入有序数组
- 633. 平方数之和
- 2824. 统计和小于目标的下标对数目
- 2563. 统计公平数对的数目
- LCP 28. 采购方案 同 2824 题
- 15. 三数之和
- 16. 最接近的三数之和
- 18. 四数之和
- 611. 有效三角形的个数
- 1577. 数的平方等于两数乘积的方法数 用双指针实现
- 923. 三数之和的多种可能 1711
- 948. 令牌放置 1762
- 11. 盛最多水的容器
- 42. 接雨水
- 1616. 分割两个字符串得到回文串 1868
- 1498. 满足条件的子序列数目 2276
- 1782. 统计点对的数目 2457
- 1099. 小于 K 的两数之和(会员题)
- 360. 有序转化数组(会员题)
- 2422. 使用合并操作将数组转换为回文序列(会员题)
- 259. 较小的三数之和(会员题)
§3.2 同向双指针
两个指针的移动方向相同(都向右,或者都向左)。
- 611. 有效三角形的个数
- 1574. 删除最短的子数组使剩余数组有序 1932
- 2972. 统计移除递增子数组的数目 II 2153
- 2122. 还原原数组 2159
- 2234. 花园的最大总美丽值 2562
- 3323. 通过插入区间最小化连通组(会员题)
相似题目:
§3.3 背向双指针
两个指针从数组中的同一个位置出发,一个向左,另一个向右,背向移动。
- 1793. 好子数组的最大分数 1946
§3.4 原地修改
- 27. 移除元素
- 26. 删除有序数组中的重复项
- 80. 删除有序数组中的重复项 II
- 283. 移动零
- 905. 按奇偶排序数组
- 922. 按奇偶排序数组 II
- 3467. 将数组按照奇偶性转化
- 2460. 对数组执行操作
- 1089. 复写零
- 75. 颜色分类
思维扩展(选做):
四、双序列双指针
§4.1 双指针
- 2109. 向字符串添加空格 1315
- 2540. 最小公共值 做到 O(n+m)
- 88. 合并两个有序数组 做到 O(n+m)
- 2570. 合并两个二维数组 - 求和法 做到 O(n+m)
- 350. 两个数组的交集 II 解决进阶问题
- LCP 18. 早餐组合
- 1855. 下标对中的最大距离 1515
- 1385. 两个数组间的距离值
- 925. 长按键入 做到 O(n+m)
- 809. 情感丰富的文字 1605
- 2337. 移动片段得到字符串 1693
- 777. 在 LR 字符串中交换相邻字符 同 2337 题
- 844. 比较含退格的字符串 做到 O(1) 额外空间
- 986. 区间列表的交集 做到 O(n+m)
- 面试题 16.06. 最小差
- 1537. 最大得分 1961
- 244. 最短单词距离 II(会员题)
- 2838. 英雄可以获得的最大金币数(会员题)
- 1229. 安排会议日程(会员题)
- 1570. 两个稀疏向量的点积(会员题)
- 1868. 两个行程编码数组的积(会员题)
§4.2 判断子序列
- 392. 判断子序列
- 524. 通过删除字母匹配到字典里最长单词
- 2486. 追加字符以获得子序列 1363
- 2825. 循环增长使字符串子序列等于另一个字符串 1415
- 1023. 驼峰式匹配 1537
- 3132. 找出与数组相加的整数 II 1620
- 522. 最长特殊序列 II 约 1700
进阶:
- 1898. 可移除字符的最大数目 1913
- 2565. 最少得分子序列 2432
- 3302. 字典序最小的合法序列 2474
五、三指针
注:部分题目已整理到「§2.3.3 恰好型滑动窗口」中。
- 2367. 等差三元组的数目 做到 O(n)
- 2563. 统计公平数对的数目 1721
- 795. 区间子数组个数 1817
- 2444. 统计定界子数组的数目 2093
- 3347. 执行操作后元素的最高频率 II 2156
- 1213. 三个有序数组的交集(会员题)
思维扩展:
- 3464. 正方形上的点之间的最大距离 2806 k 个指针
六、分组循环
适用场景:按照题目要求,数组会被分割成若干组,每一组的判断/处理逻辑是相同的。
核心思想:
- 外层循环负责遍历组之前的准备工作(记录开始位置),和遍历组之后的统计工作(更新答案最大值)。
- 内层循环负责遍历组,找出这一组最远在哪结束。
这个写法的好处是,各个逻辑块分工明确,也不需要特判最后一组(易错点)。以我的经验,这个写法是所有写法中最不容易出 bug 的,推荐大家记住。
- 1446. 连续字符 1165
- 1869. 哪种连续子字符串更长 1205
- 2414. 最长的字母序连续子字符串的长度 1222
- 3456. 找出长度为 K 的特殊子字符串 1244
- 1957. 删除字符使字符串变好 1358
- 674. 最长连续递增序列
- 978. 最长湍流子数组 1393
- 2110. 股票平滑下跌阶段的数目 1408
- 228. 汇总区间
- 2760. 最长奇偶子数组 1420
- 1887. 使数组元素相等的减少操作次数 1428
- 845. 数组中的最长山脉 1437
- 2038. 如果相邻两个颜色均相同则删除当前颜色 1468
- 2900. 最长相邻不相等子序列 I 1469
- 1759. 统计同质子字符串的数目 1491
- 3011. 判断一个数组是否可以变为有序 1497
- 1578. 使绳子变成彩色的最短时间 1574
- 1839. 所有元音按顺序排布的最长子字符串 1580
- 2765. 最长交替子数组 1581
- 3255. 长度为 K 的子数组的能量值 II 1595
- 3350. 检测相邻递增子数组 II 1600
- 3105. 最长的严格递增或递减子数组
- 135. 分发糖果
- 838. 推多米诺 1638
- 467. 环绕字符串中唯一的子字符串 约 1700
- 3499. 操作后最大活跃区段数 I 1729
- 2948. 交换得到字典序最小的数组 2047
- 2593. 标记所有元素后数组的分数 做到 O(n)
- 2393. 严格递增的子数组个数(会员题)
- 2436. 使子数组最大公约数大于一的最小分割数(会员题)
- 2495. 乘积为偶数的子数组数(会员题)
- 3063. 链表频率(会员题)
思考
做了一些题目后,请总结:滑动窗口和双指针的区别是什么?
欢迎在评论区发表你的做题总结。
关联题单
算法题单
- 滑动窗口与双指针(定长/不定长/单序列/双序列/三指针/分组循环)
- 二分查找(二分答案/最小化最大值/最大化最小值/第K小)
- 单调栈(基础/矩形面积/贡献法/最小字典序)
- 网格图(DFS/BFS/综合应用)
- 位运算(基础/性质/拆位/试填/恒等式/思维)
- 图论算法(DFS/BFS/拓扑排序/基环树/最短路/最小生成树/网络流)
- 动态规划(入门/背包/划分/状态机/区间/状压/数位/数据结构优化/树形/博弈/概率期望)
- 常用数据结构(前缀和/差分/栈/队列/堆/字典树/并查集/树状数组/线段树)
- 数学算法(数论/组合/概率期望/博弈/计算几何/随机算法)
- 贪心与思维(基本贪心策略/反悔/区间/字典序/数学/思维/脑筋急转弯/构造)
- 链表、二叉树与回溯(前后指针/快慢指针/DFS/BFS/直径/LCA/一般树)
- 字符串(KMP/Z函数/Manacher/字符串哈希/AC自动机/后缀数组/子序列自动机)
如果你发现有题目可以补充进来,欢迎评论反馈。