Typescript-Algorithms
    Preparing search index...

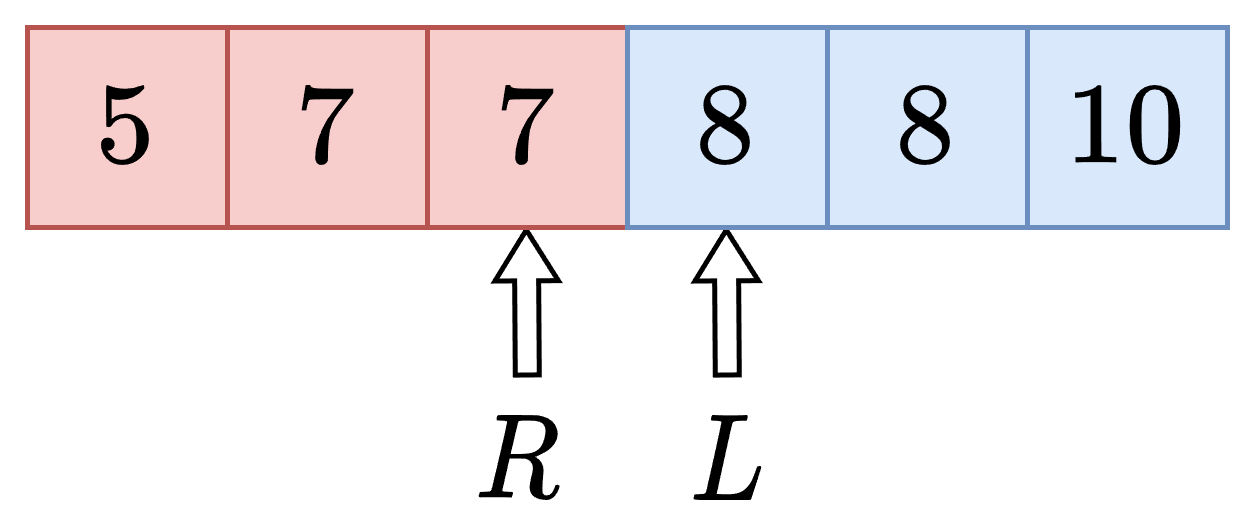
    二分题单二分查找二分查找二分入门二分题目力扣二分 leetcode 二分

    图：闭区间二分循环结束时的左右指针位置（查找第一个 8）

    题目已按照难度分排序，右侧数字为难度分。

    如果遇到难度很大，题解都看不懂的题目，建议直接收藏，过段时间再来做。

    请先学习：二分查找 红蓝染色法【基础算法精讲 04】

    部分题目需要先排序，然后在有序数组上二分查找。

    思维扩展：

    “花费一个 log 的时间，增加了一个条件。” —— 二分答案

    题目求什么，就二分什么。

    问：如何把二分答案与数组上的二分查找联系起来？

    答：假设答案在区间 [2,5] 中，我们相当于在一个虚拟数组 [check(2),check(3),check(4),check(5)] 中二分找第一个（或者最后一个）值为 true 的 check(i)。这同样可以用红蓝染色法思考。

    问：有些题目，明明 m 可以是答案，但却不在初始二分区间中。比如闭区间二分初始化 right=m−1（或者开区间 right=m），这不会算错吗？

    答：不会算错。注意「答案所在区间」和「二分区间」是两个概念。想一想，如果二分的 while 循环每次更新的都是 left，那么最终答案是什么？正好就是 m。一般地，如果一开始就能确定 m 一定可以满足题目要求，那么 m 是不需要在二分区间中的。换句话说，二分区间是「尚未确定是否满足题目要求」的数的范围。那些在区间外面的数，都是已确定的满足（不满足）题目要求的数。

    问：什么是循环不变量？

    答：想一想，对于求最小的题目，开区间二分的写法，为什么最终返回的是 right，而不是别的数？在初始化（循环之前）、循环中、循环结束后，都时时刻刻保证 check(right) == true 和 check(left) == false，这就叫循环不变量。根据循环不变量，循环结束时 left + 1 == right，那么 right 就是最小的满足要求的数（因为再 −1 就不满足要求了），所以答案是 right。

    注：部分题目可以优化二分边界，减少二分次数，从而减少代码运行时间。对于初次接触二分答案的同学，无需强求自己写出最优的代码，设定一个比较大的二分上界也是可以的。

    思维扩展：

    一图掌握二分答案！四种写法！

    在练习时，请注意「求最小」和「求最大」的二分写法上的区别。

    前面的「求最小」和二分查找求「排序数组中某元素的第一个位置」是类似的，按照红蓝染色法，左边是不满足要求的（红色），右边则是满足要求的（蓝色）。

    「求最大」的题目则相反，左边是满足要求的（蓝色），右边是不满足要求的（红色）。这会导致二分写法和上面的「求最小」有一些区别。

    以开区间二分为例：

    • 求最小：check(mid) == true 时更新 right = mid，反之更新 left = mid，最后返回 right。
    • 求最大：check(mid) == true 时更新 left = mid，反之更新 right = mid，最后返回 left。

    对于开区间写法，简单来说 check(mid) == true 时更新的是谁，最后就返回谁。相比其他二分写法，开区间写法不需要思考加一减一等细节，推荐使用开区间写二分。

    二分的不是答案，而是一个和答案有关的值（间接值）。

    本质是二分答案求最小。二分的 mid 表示上界。

    本质是二分答案求最大。二分的 mid 表示下界。

    例如数组 [1,1,1,2,2]，其中第 1 小、第 2 小和第 3 小的数都是 1，第 4 小和第 5 小的数都是 2。

    • 第 k 小等价于：求最小的 x，满足 ≤x 的数至少有 k 个。
    • 第 k 大等价于：求最大的 x，满足 ≥x 的数至少有 k 个。

    注 1：一般规定 k 从 1 开始，而不是像数组下标那样从 0 开始。

    注 2：部分题目也可以用堆解决。

    二分答案的一个难点是 check 函数怎么写，这会涉及到贪心等技巧，可以练练下面的贪心题单（主要是第一章节）。

    如何科学刷题？

    1. 滑动窗口与双指针（定长/不定长/单序列/双序列/三指针/分组循环）
    2. 二分查找（二分答案/最小化最大值/最大化最小值/第K小）
    3. 单调栈（基础/矩形面积/贡献法/最小字典序）
    4. 网格图（DFS/BFS/综合应用）
    5. 位运算（基础/性质/拆位/试填/恒等式/思维）
    6. 图论算法（DFS/BFS/拓扑排序/基环树/最短路/最小生成树/网络流）
    7. 动态规划（入门/背包/划分/状态机/区间/状压/数位/数据结构优化/树形/博弈/概率期望）
    8. 常用数据结构（前缀和/差分/栈/队列/堆/字典树/并查集/树状数组/线段树）
    9. 数学算法（数论/组合/概率期望/博弈/计算几何/随机算法）
    10. 贪心与思维（基本贪心策略/反悔/区间/字典序/数学/思维/脑筋急转弯/构造）
    11. 链表、二叉树与回溯（前后指针/快慢指针/DFS/BFS/直径/LCA/一般树）
    12. 字符串（KMP/Z函数/Manacher/字符串哈希/AC自动机/后缀数组/子序列自动机）

    我的题解精选（已分类）

    欢迎关注 B站@灵茶山艾府

    如果你发现有题目可以补充进来，欢迎评论反馈。

    Settings

    Member Visibility

    On This Page

    一、二分查找二、二分答案三、其他关联题单算法题单